PENGERTIAN POLA BILANGAN DAN JENIS-JENIS POLA BILANGAN

Nuu kali ini mulai keliatan serius ya blognya, tapi ga serius-serius amat sih. Nah hari ini saya mau share buat teman-teman semua kali aja ada yang membutuhkan. Sebenarnya materi ini "salah satu" materi yang saya ajukan untuk penelitian skripsi, tapi karena sesuatu dan lain hal kagak jadi hayati penelitian pake materi ini. Sedih sih iya, tapi life must going on, iya toh?
Nah, dari pada mubazir ni, hayati udah ngumpulin, ngeringkas, ngeprint dan sebagainya untuk bahan penelitian yang kagak jadi, mending hayati bagiin aja di mari. Ashiaap, nah ini untuk materinya aja dulu, untuk contoh soalnya dan Mind Mapping-nya nyusul yesss. Stay tuned!

Pengertian Pola Bilangan

Pola dapat diartikan sebagai sebuah susunan yang mempunyai bentuk teratur dari bentuk yang satu ke bentuk berikutnya. Sedangkan bilangan adalah sesuatu yang digunakan untuk menunjukkan kuantitas (banyak, sedikit) dan ukuran (berat, ringan, panjang, pendek, luas) suatu objek. Bilangan ditunjukkan dengan suatu tanda atau lambang yang disebut angka. 
Sehingga pola bilangan dapat diartikan sebagai susunan angka-angka yang mempunyai bentuk teratur dari bentuk yang satu ke bentuk berikutnya. 

Jenis-jenis Pola Bilangan

1. Pola Garis Lurus

Penulisan bilangan yang mengikuti pola garis lurus merupakan pola bilangan yang paling sederhana. Suatu bilangan hanya digambarkan dengan noktah yang mengikuti pola garis lurus. Misalnya
o o           mewakili bilangan dua
o o o        mewakili bilangan tiga
o o o o     mewakili bilangan empat, dan seterusnya

2. Pola  Bilangan Ganjil

Bilangan ganjil adalah bilangan asli yang tidak habis dibagi 2. Bilangan ganjil diawali dengan bilangan 1 dan bilangan selanjutnya memiliki selisih 2 dengan bilangan sebelumnya. 

•  Pola bilangan ganjil memiliki pola 1, 3, 5, 7, 9 ….
•  Barisan bilangan ganjil adalah 1,3, 5, 7, 9, …
•  Deret bilangan ganjil adalah 1 + 3 + 5 + 7 + 9 + ….
•  Rumus mencari suku ke ke-n adalah Un = 2n – 1, Dengan: Un = suku yang ditanya, n = angka ke
   berapa?,
•  Rumus mencari jumlah n suku pertama adalah Sn = n2, dengan Sn = jumlah bilangan sebanyak n
   buah.
•  Berikut adalah gambar pola dari bilangan ganjil

Contoh:
1 , 3 , 5 , 7 , . . . , ke 10.
Berapakah pola bilangan ganjil ke 10 ?
Jawab :
Un = 2n – 1
U10 = 2 . 10 – 1
        = 20 – 1   = 19
3. Pola  Bilangan Genap

Bilangan genap adalah bilangan asli yang habis dibagi 2. Bilangan genap diawali dengan bilangan 2 dan bilangan selanjutnya memiliki selisih 2 dengan bilangan sebelumnya. 

• Pola bilangan genap adalah 2, 4, 6, 8, 10, …..
• Barisan bilangan genap adalah 2, 4, 6, 8, 10, ….
• Deret bilangan genap adalah 2 + 4 + 6 + 8 + 10 + …..
• Rumus untuk mencari suku ke-n adalah Un = 2n
• Rumus mencari jumlah n suku pertama adalah Sn = n2 + n
• Gambar pola bilangan genap adalah sebagai berikut

Contoh:
Dari barisan bilangan berikut. 2,4,6...
a) Tentukan angka suku ke 325. 
b) 840 merupakan suku (angka ke)...
c) Tentukan jumlah 21 suku pertama.
Penyelesaian:
a) n = 325. 
Un = 2n  = 2(325).   
Un = 650
b) Un =840. 
Un = 2n =840.   n = 420.        c) n= 21.  Sn = n2 + n = n2 + n = 212 + 21= 462.

4. Pola Bilangan Persegi

 Pola bilangan persegi adalah 1, 4, 9, 16, 25, …..

 Barisan bilangan persegi adalah 1, 4, 9, 16, 25, …..

 Deret bilangan persegi adalah 1 + 4 + 9 + 16 + 25 + ……

 Rumus mencari suku ke-n adalah Un = n2

 Rumus mencari jumlah n suku pertama adalah Sn = 1/6 n ( n + 1 ) ( 2n + 1 )

 Gambar pola bilangan persegi adalah sebagai berikut

5. Pola bilangan segitiga

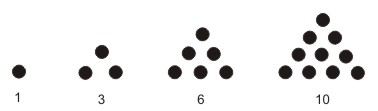
 Pola bilangan segitiga adalah 1, 3, 6, 10, 15, 21, …..
 Barisan bilangan segitiga adalah 1, 3, 6, 10, 15, 21, …..
 Deret bilangan segitiga adalah 1 + 3 + 6 + 10 + 15 + 21 + …..
 Rumus mencari suku ke-n adalah Un = ½ n (n + 1 )
 Rumus mencari jumlah n suku pertama adalah Sn = 1/6 n ( n + 1 ) ( n + 2 )
 Gambar pola bilangan segitiga adalah sebagai berikut

6. Pola bilangan persegi panjang

 Pola bilangan persegi panjang adalah 2, 6, 12, 20, 30, ……
 Barisan bilangan persegi panjang adalah 2, 6, 12, 20, 30, ……
 Deret bilangan persegi panjang adalah 2 + 6 + 12 + 20 + 30 + …..
 Rumus mencari suku ke-n adalah Un = n ( n + 1 )
 Rumus mencari jumlah n suku pertama adalah Sn = 1/3 n ( n + 1 ) ( n + 2 )
 Gambar pola bilangan persegi panjang adalah sebagai berikut

 

7. Pola Bilangan Kubus

 Pola kubus terbentuk dari bilangan kubik Un = n3.
 Barisan: 1, 8, 27, 64, 125, 216, …
 Deret: 1 + 8 + 27 + 64 + 125 + 216 + …
 Rumus Suku ke-n: Un = n³
 Jumlah n suku pertama: Sn = 1/4 n² ( n + 1 )²

8. Pola bilangan segitiga Pascal

 Adapun aturan-aturan untuk membuat pola segitiga Pascal adalah sebagai berikut:

          a. Angka 1 merupakan angka awal yang terdapat di puncak.

          b. Simpan dua bilangan di bawahnya. Oleh karena angka awal dan akhir selalu angka 1, kedua
              bilangan tersebut adalah 1.

  c. Selanjutnya, jumlahkan bilangan yang berdampingan. Kemudian, simpan hasilnya di bagian
              tengah bawah kedua bilangan tersebut.

  d. Proses ini dilakukan terus sampai batas susunan bilangan yang diminta.

 Pola segitiga Pascal merupakan pola 2n dengan n bilangan bulat. Suku berikutnya dapat dicari
        dari hasil kali 2 dengan suku sebelumnya.

 Rumus mencari jumlah baris ke-n adalah 2n – 1

 Gambar pola bilangan segitiga pascal adalah sebagai berikut

S1 = 1 diperoleh dari S1 = 1 = 20

S2 = 2 diperoleh dari S2 = 1 + 1 = 2 = 21

S3 = 4 diperoleh dari S3 = 1 + 2 + 1 = 4 = 22

S4 = 8 diperoleh dari S4 = 1 + 3 + 3 + 1 = 8 = 23

S5 = 16 diperoleh dari S5 = 1 + 4 + 6 + 4 + 1 = 16 = 24

Jadi, dapat disimpulkan bahwa rumus mencari jumlah suku ke-n adalah Sn = 2n-1.

9. Pola bilangan Fibonacci

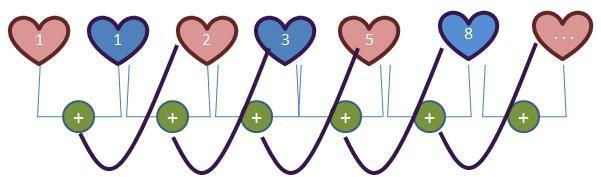
 Pola bilangan fibanocci adalah pola bilangan dimana jumlah bilangan setelahnya merupakan
        hasil dari penjumlahan dari dua bilangan sebelumnya.

 Pola bilangan Fibonacci adalah 1, 1, 2, 3, 5, 8, 13, 21, 34, ..., ...        

        U1 = 0 + 1 = 1

        U2 = 1 + 1 = 2

        U3 = 1 + 2 = 3

        Un = penjumlahan dua bilangan didepannya     

 Rumus mencari suku ke-n adalah Un = Un – 1 + Un - 2

 Gambar pola bilangan persegi panjang adalah sebagai berikut